Решение задач по сопромату № 217365

Дисциплина: «Сопромат»
Решение задач по сопромату № 217365
Цена 250 руб.

Задача 1

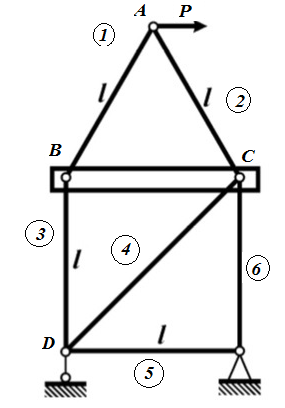
Для плоской фермы, содержащей деформируемые стержни и абсолютно жесткие элементы, построить эпюру нормальных сил в стержнях.
Дано: F/P=1, F=P
Решение:
1. Рассмотрим равновесие узла А

Задача 2
Консольный стержень нагружен равномерно распределенными нагрузками интенсивностью q1 и q2 и сосредоточенными силами F1 и F2. Построить эпюру нормальной силы.
Дано: F1/ql=1,5, F2/ql =2, l1/l=2, q1/q=-1, l2/l=2
Решение:
Применяя метод сечений, устанавливаем законы изменения продольных сил по длине каждого из участков бруса.

Задача 3
Вал находится в равновесии под действием двух пар сил моментами М1и М2 и двух равномерно распределенных по длине стержня моментов интенсивностью m1 и m2. Построить эпюру крутящего момента в долях ml.
Дано: М1/ml=2, M2/ml =1, l1/l=2, l2/l=1, m1/m=-1, m2/m=1,5
Решение.
При определении крутящего момента применяем метод сечений. Проводя мысленно сечение в пределах каждого из участков, отбрасываем

Задача 4
Для балки построить эпюры поперечной силы и изгибающего момента.
Дано: F/ql=2, q1/q=2, l1/l=1, l2/l=2, M/ql2=1
Решение:
1) Опорные реакции.

Задача 5
Для консольной балки построить эпюры поперечной силы и изгибающего момента.
Дано: F/ql=2, q1/q=-1, q2/q=1, l1/l=1, l2/l=1, M/ql2=-1
Решение:
1. Построение эпюр. Разобьём балку на участки. С помощью метода сечений найдем величину поперечной силы QY и изгибающего момента МX на