Контрольная по электротехнике и электронике 2-Вариант три задачи № 200417

Дисциплина: «Электротехника и электроника»

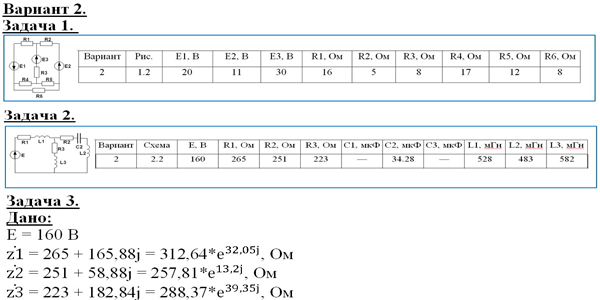
Задача 1.
Расчетная схема.

Дано:
E1 = 20 В; E2 = 11 В; E3 = 30 В
R1 = 16 Ом; R2 = 5 Ом; R3 = 8 Ом
R4 = 17 Ом; R5 = 12 Ом; R6 = 8 Ом
Найти: Согласно заданию.Определить токи в цепи
Решение

1. Кирхгоф.
Согласно 1-му закону Кирхгофа для узлов:
Cистема 1:
Согласно 2-му закону Кирхгофа для контуров:
Обход контуров по часовой стрелке.
Cистема 2:
Подставим значения в системы (1) и (2):
2. Расчет схемы.
Воспользуемся уже составленной системой (3)
Решаем методом Крамера.
Матрица коэффициентов |A|:
Вектор свободных членов |B|:
Определители переменных:
(которые являются определителями матриц, полученных из матрицы А заменой
k — ого столбца (k = 1, 2, …, n) на столбец свободных членов)
Решение системы (|A|*|X| = |B|)
Токи ветвей:
3. Баланс мощностей.
Мощность, потребляемая нагрузкой, должна совпадать с мощностью, генерируемой источниками — закон сохранения энергии.
Исходные данные:
3. 1. Нагрузка:
Мощность, выделяемую в нагрузке определяем как:
3. 2. Источник:
Мощность, генерируемая источниками ЭДС:
3. 3. Выводы:
1. Баланс сошелся. Задача решена верно.

Задача 2.
расчет однофазной цепи синусоидального тока
Определить токи, напряжения, мощности на всех участках и во всей цепи.
Расчетная схема:

Дано:
E = 160 В
R1 = 265 Ом; L1 = 528 мГн
R2 = 251 Ом; L2 = 483 мкФ; C2 = 34,28 мкФ
R3 = 223 Ом; L3 = 582 мГн
Найти: В соответствии с заданием.

1. Параметры элементов цепи:
Комплексные сопротивления ветвей:
Эквивалентное комплексное сопротивление параллельных ветвей:
Эквивалентное комплексное сопротивление цепи:
2. Токи ветвей:
Ток в неразветвленной части цепи:
Напряжение на параллельных ветвях:
Токи параллельных ветвей:
3. Напряжения на элементах ветвей:
4. Мощность.
4. 1. Мощность ветвей:
Расчет ведем по выражению:
4. 2. Итого по нагрузке:
4. 3. Мощность источника:
Расчет ведем по выражению:
4. 4. Погрешность расчета:
Баланс сошелся, задача решена верно.
5. Векторная диаграмма:
Используем ранее рассчитанные значения Ui.
Масштаб по току mI: 1 дел. — 0,1 А
Масштаб указан по ГОСТу для случая, когда длина единичного (клетка)

Задача 3.
Дано:
E = 160 В
(z1) ̇ = 265 + 165,88j = 312,64*e^32,05j, Ом
(z2) ̇ = 251 + 58,88j = 257,81*e^13,2j, Ом
(z3) ̇ = 223 + 182,84j = 288,37*e^39,35j, Ом
Рассчитать линейную электрическую цепь с несинусоидальной ЭДС, изменяющейся по закону:

Источник:
Здесь и далее индекс соответствует номеру гармоники.
1. Параметры элементов цепи для ω_((3)):
Эквивалентное комплексное сопротивление параллельных ветвей:
Эквивалентное комплексное сопротивление цепи:
2. Токи ветвей:
Ток в неразветвленной части цепи:
Напряжение на параллельных ветвях:
Токи параллельных ветвей:
3. Расчет постоянной составляющей.
Учтем, что на постоянном токе в установившемся режиме индуктивность
4. Итог расчета.
Действующее значение тока и напряжения определяем как:
5. По результатам расчета построить графики изменения токов в ветвях.
Контрольная по электротехнике и электронике 2-Вариант три задачи № 200417
Цена 350 р.